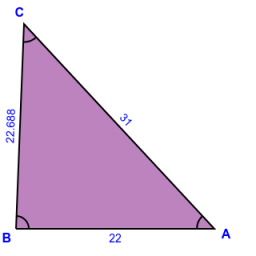
SAS calculation
Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle A is 47°, find side a. Please round to one decimal.
Correct answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Measurements of a triangle
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft - Trapezoid 7537
Diagonal alpha equals 0.4 m, and diagonal beta equals 0.4 m in the isosceles trapezoid. Side AB is 120 cm, and side DC is 7.6 dm. Find the length of arms in an isosceles trapezoid. Please result round to 2 decimal places. - Calculate
Calculate the area of triangle ABC if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm. - Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t
- Gamma angle
Find the magnitude of the gamma angle in triangle ABC if: α = 38° 56' and β = 47° 54'. - Circle arc
Calculate the circular arc area in m² where the diameter is 263 dm and the central angle is 40°. Please result round to three decimal places. - Triangles
Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3'
