Square practice problems - page 148 of 150

Number of problems found: 2994

Truncated pyramid
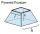The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
The tower
The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter.
Quarter circle
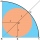What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
Circle sector
The circular sector with a central angle 160° has an area 452 cm². Calculate its radius r.
Circular park
The circular park has an area of 1600 m². Cross the park, right in its center, leads the trail. What is the length of the trail?
Tunnel boring
How much material did they dig when cutting the 400m long tunnel? The area of the circular segment, which is the cross-section of the tunnel, is 62m².
Hexa pyramid
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high.
Trapezoid
Are diagonals in a rectangular trapezoid perpendicular and bisect the angles?
Spherical segment
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
Quadrilateral prism
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
Rectangular trapezoid
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
Circular segment
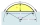A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius?
Arc-sector
arc length = 17 cm area of sector = 55 cm² arc angle = ? the radius of the sector = ?
A cell tower
A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal?
Perpendicular sides
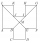In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ
Goat
The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent
Area 4gon
Calculate the area of 4-gon, two, and the two sides are equal and parallel with lengths 18, 9, 18, and 9. Inner angles are 45°, 135°,45°, 135°.
Circular arc
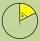Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm²
Coordinates hexagon
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle.
The cone
The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (The cone side is the segment joining the vertex cone with any point of the base circle. All sides

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.