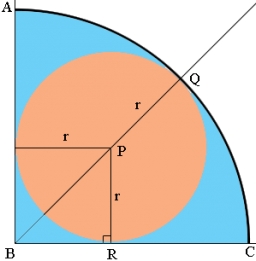
Quarter circle
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
Correct answer:
Showing 1 comment:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Inscribed 7018
The dragon has the shape of a regular hexagon inscribed in a circle with a radius of 20 cm. What is the area of the dragon? - Hexagon
Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter? - Inscribed circle
A circle is inscribed in the triangle with sides of 13 cm, 14 cm, and 15 cm. What is its radius? - Company logo
The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
- Calculate 25621
Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm. - ET inscribed circle
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Square inscribed
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
