Company logo

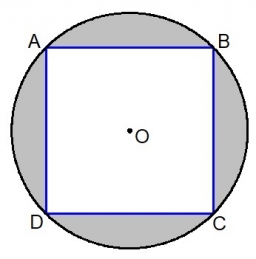
The company logo consists of a blue circle with a radius of 4 cm, which is an inscribed white square. What is the area of the blue part of the logo?

Correct result:

S =  18.2655 cm2

Solution:

r=4 cm u=2⋅ r=2⋅ 4=8 cm D=u=8=8 cm  D2=a2+a2  a=D/2=8/2=4 2 cm≐5.6569 cm  S1=π⋅ r2=3.1416⋅ 42≐50.2655 cm2 S2=a2=5.65692=32 cm2  S=S1−S2=50.2655−32=18.2655 cm2

Try another example


We would be very happy if you find an error in the example, spelling mistakes, or inaccuracies, and please send it to us. We thank you!






Showing 0 comments:
avatar




Tips to related online calculators
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:


 
We encourage you to watch this tutorial video on this math problem: video1   video2

Next similar math problems:

  • Waste
    doska_kruh How many percents are waste from a circular plate with a radius of 1 m from which we cut a square with the highest area?
  • Two circles
    intersect_circles Two circles with the same radius r = 1 are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles?
  • Circular ring
    mezikruzi Square with area 16 centimeters square are inscribed circle k1 and described circle k2. Calculate the area of circular ring, which circles k1, k2 form.
  • Chord 2
    circle_ Point A has distance 13 cm from the center of the circle with radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle.
  • An equilateral
    goat__wolf_and_cabbage_1 An equilateral triangle with a side 10 m represents a wooden platform standing in a lawn. A goat is tied to a corner with a 15 m rope. What is the maximum amount of grazing area available to the goat?
  • Logs
    tramy The log has diameter 30 cm. What's largest beam with a rectangular cross-section can carve from it?
  • Round table
    obrus-kruhovy Round table with diameter d = 105 cm is coated by square tablecloth with a side length 121 cm. About how many cm is higher center of tablecloth than its cornes?
  • RT - inscribed circle
    rt_incircle In a rectangular triangle has sides lengths> a = 30cm, b = 12.5cm. The right angle is at the vertex C. Calculate the radius of the inscribed circle.
  • Square diagonal
    square_diagonal Calculate the length of diagonal of the square with side a = 23 cm.
  • Square
    1square Calculate area of the square with diagonal 64 cm.
  • Isosceles triangle
    rr_triangle3_1 Calculate the area of an isosceles triangle, the base of which measures 16 cm and the arms 10 cm.
  • Double ladder
    dvojak The double ladder is 8.5m long. It is built so that its lower ends are 3.5 meters apart. How high does the upper end of the ladder reach?
  • Center traverse
    trianles It is true that the middle traverse bisects the triangle?
  • Double ladder
    rr_rebrik The double ladder shoulders should be 3 meters long. What height will the upper top of the ladder reach if the lower ends are 1.8 meters apart?
  • The trapezium
    rt_iso_triangle The trapezium is formed by cutting the top of the right-angled isosceles triangle. The base of the trapezium is 10 cm and the top is 5 cm. Find the area of trapezium.
  • Diamond area from diagonals
    kosostvorec In the diamond ABCD is AB = 4 dm and the length of the diagonal is 6.4 dm long. What is the area of the diamond?
  • Tree trunk
    tram From the tree trunk, the diameter at the narrower end is 28 cm, a beam of square cross-section is to be made. Calculate the longest side of the largest possible square cross-section.