Silver medal

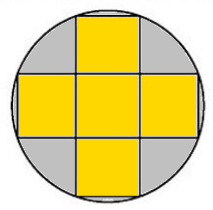
A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part?

b) What is the area of the Golden Cross?

Final Answer:

S =  28.54 cm²
S₅ =  50 cm²

Step-by-step explanation:

$$\begin{gathered} D=10\text{cm} \\ r=D/2=10/2=5\text{cm} \\ {D}^2=a^2+(3a{)}^2 \\ {D}^2=a^2+9a^2 \\ {D}^2=10a^2 \\ D=\sqrt{10}a \\ a=D/\sqrt{10}=10/\sqrt{10}=\sqrt{10}\text{cm}\doteq 3.1623\text{cm} \\ n=5 \\ {S}_5=n\cdot a^2=5\cdot 3.1623^2=50{\text{cm}}^2 \\ {S}_2=\pi \cdot r^2=3.1416\cdot 5^2\doteq 78.5398{\text{cm}}^2 \\ S=S_2-S_5=78.5398-50\doteq 28.5398{\text{cm}}^2 \\ \text{ Verifying Solution: } \\ {S}_3=\frac{5}{5+1/2+1/2}\cdot S_2=\frac{5}{5+1/2+1/2}\cdot 78.5398\doteq 65.4498{\text{cm}}^2 \\ {S}_5\doteq S \end{gathered}$$

Try another example