Square practice problems - page 42 of 150
Number of problems found: 2994
- Axial symmetry
 Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number)
Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number) - Calculate 8
 Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0. - Equilateral 83013
 Traffic signs are equilateral triangles with a side length of 900 mm. How many euros does a galvanized sheet cost to produce 50 pieces of such brands if we consider adding 15% of the material for waste? The price of 1 square meter of sheet metal is 6.5 eu
Traffic signs are equilateral triangles with a side length of 900 mm. How many euros does a galvanized sheet cost to produce 50 pieces of such brands if we consider adding 15% of the material for waste? The price of 1 square meter of sheet metal is 6.5 eu - Vector - basic operations
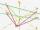 There are given points A [-9; -2] B [2; 16] C [16; -2] and D [12; 18] a. Determine the coordinates of the vectors u=AB v=CD s=DB b. Calculate the sum of the vectors u + v c. Calculate the difference of vectors u-v d. Determine the coordinates of the vecto
There are given points A [-9; -2] B [2; 16] C [16; -2] and D [12; 18] a. Determine the coordinates of the vectors u=AB v=CD s=DB b. Calculate the sum of the vectors u + v c. Calculate the difference of vectors u-v d. Determine the coordinates of the vecto - Displacement 55871
 Assemble the two offsets, d1, and d2, shown by OA and OB oriented lines. The coordinates of the points are O = (0m, 0m), A = (3m, 3m), and B = (5m, 2m). Measure the magnitude of the resulting displacement d.
Assemble the two offsets, d1, and d2, shown by OA and OB oriented lines. The coordinates of the points are O = (0m, 0m), A = (3m, 3m), and B = (5m, 2m). Measure the magnitude of the resulting displacement d. - Curve and line
 The equation of a curve C is y=2x² -8x+9, and the equation of a line L is x+ y=3 (1) Find the x coordinates of the points of intersection of L and C. (2) Show that one of these points is also the stationary point of C?
The equation of a curve C is y=2x² -8x+9, and the equation of a line L is x+ y=3 (1) Find the x coordinates of the points of intersection of L and C. (2) Show that one of these points is also the stationary point of C? - Intersection of Q2 with line
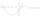 The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the
The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - A car
 A car weighing 1.05 tonnes, driving at the maximum allowed speed in the village (50 km/h), hits a solid concrete bulkhead. Calculate the height that would have to fall on the concrete surface to make the impact intensity the same as in the first case!
A car weighing 1.05 tonnes, driving at the maximum allowed speed in the village (50 km/h), hits a solid concrete bulkhead. Calculate the height that would have to fall on the concrete surface to make the impact intensity the same as in the first case! - Determine 83003
 Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common.
Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common. - Perpendicular 82994
 The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis.
The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis. - Perpendicular projection
 Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0.
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0. - On a line
 On a line p : 3 x - 4 y - 3 = 0, determine the point C equidistant from points A[4, 4] and B[7, 1].
On a line p : 3 x - 4 y - 3 = 0, determine the point C equidistant from points A[4, 4] and B[7, 1]. - Square
 Draw a square on the edge of a = 4 cm. Mark the center of symmetry S and all axes of symmetry. How many axes of symmetry do you have? Write down.
Draw a square on the edge of a = 4 cm. Mark the center of symmetry S and all axes of symmetry. How many axes of symmetry do you have? Write down. - The farmer
 The farmer would like to first seed his small field. The required amount depends on the seed area. The field has a triangular shape. The farmer had a fenced field, so he knew the lengths of the sides: 73, 117, and 63 meters. Find a suitable way to determi
The farmer would like to first seed his small field. The required amount depends on the seed area. The field has a triangular shape. The farmer had a fenced field, so he knew the lengths of the sides: 73, 117, and 63 meters. Find a suitable way to determi - Intersections 62784
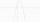 A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3
A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - Rectangular 75334
 In the rectangular coordinate system, find the images of points A[-3; 2] and B[4; -5] in central symmetry according to point O[0; 0]. A. A'[3; 2], B'l-4; -5] C. A'[-3; -2], B'[4; 5] B. A'[-3; -2], B'[-4; 5] D. A'[3; -2], B'[-4; 5]
In the rectangular coordinate system, find the images of points A[-3; 2] and B[4; -5] in central symmetry according to point O[0; 0]. A. A'[3; 2], B'l-4; -5] C. A'[-3; -2], B'[4; 5] B. A'[-3; -2], B'[-4; 5] D. A'[3; -2], B'[-4; 5] - Isosceles
 A flower bed has the shape of an isosceles triangle with a base of 25m and sides of 30m. Calculate the maximum number of flowers that can be planted in this bed, assuming that one flower requires about 8 dm² of square area. Round the result to the nearest
A flower bed has the shape of an isosceles triangle with a base of 25m and sides of 30m. Calculate the maximum number of flowers that can be planted in this bed, assuming that one flower requires about 8 dm² of square area. Round the result to the nearest - Parabola
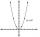 Find the equation of a parabola that contains the points at A[10; -5], B[18; -7], C[20; 0]. (use y = ax²+bx+c)
Find the equation of a parabola that contains the points at A[10; -5], B[18; -7], C[20; 0]. (use y = ax²+bx+c) - Coordinates 83025
 Given are points A [1;a2;a3], B [3;-4;-1], C [-3;-1;8]. Points A, B, and C lie in a straight line. Calculate the coordinates a2, a3
Given are points A [1;a2;a3], B [3;-4;-1], C [-3;-1;8]. Points A, B, and C lie in a straight line. Calculate the coordinates a2, a3 - Calculate 7344
 Draw squares. Color them and calculate the perimeter and areas square ABCD a = 3cm square EFGH b = 4cm
Draw squares. Color them and calculate the perimeter and areas square ABCD a = 3cm square EFGH b = 4cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
