Calculate 8
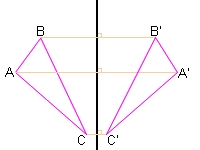
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
Correct answer:
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Coordinates 83482
I have a point A=[2,1] and a line y+x-5=0. How do I determine the coordinates of point A', which is the image of point A according to the given straight line? - Perpendicular projection
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0. - Circle
From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and the radius of the circle r. - Parametric form
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
- On line
On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0]. - Coordinates 83025
Given are points A [1;a2;a3], B [3;-4;-1], C [-3;-1;8]. Points A, B, and C lie in a straight line. Calculate the coordinates a2, a3 - Determine 82478
Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line.
