Surface area of Sphere Problems - page 2 of 5
Number of problems found: 88
- Hemispherical dome
 What is the coverage area of the painting of a hemispherical dome with a diameter of 8 m?
What is the coverage area of the painting of a hemispherical dome with a diameter of 8 m? - Spherical cap
 What is the surface area of a spherical cap, the base diameter 27 m, and height 2 m?
What is the surface area of a spherical cap, the base diameter 27 m, and height 2 m? - Cubes
 One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm².
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - Big Earth
 What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km. - Decorations - spherical
 The glass Christmas decorations have the shape of a ball with a diameter of 8 cm. In a small family business, they produce 50,000 pieces a year. The entire surface of these balls is covered with glitter. 400 g of glitter is needed to cover an area of 1 m²
The glass Christmas decorations have the shape of a ball with a diameter of 8 cm. In a small family business, they produce 50,000 pieces a year. The entire surface of these balls is covered with glitter. 400 g of glitter is needed to cover an area of 1 m² - Larger sphere
 The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³.
The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³. - Sphere in cone
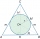 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Hectoliters - reservoir
 The reservoir has the shape of a sphere with a diameter of 10 m. How many hectoliters of water is in it when it is filled to 90%? How many kg of paint are needed for painting if it is painted twice, and 1 kg of paint is enough for 6 square meters?
The reservoir has the shape of a sphere with a diameter of 10 m. How many hectoliters of water is in it when it is filled to 90%? How many kg of paint are needed for painting if it is painted twice, and 1 kg of paint is enough for 6 square meters? - Cube from sphere
 What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm?
What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm? - Material consumption
 The sphere-shaped reservoir has a volume of 282 hl. Calculate the material consumption in m² for its production, assuming 8% for joints and waste, and round the final result to the nearest integers.
The sphere-shaped reservoir has a volume of 282 hl. Calculate the material consumption in m² for its production, assuming 8% for joints and waste, and round the final result to the nearest integers. - The observatory
 The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste?
The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste? - Tropical, mild and arctic
 How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'.
How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'. - Spherical sector
 The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector.
The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector. - Reservoir - water tank
 The reservoir has the shape of a sphere with a diameter of 14 m. a) How many hectoliters (hl) of water can it hold? b) How many kg of paint is needed to paint the reservoir if it is painted three times and one kg of paint is enough to paint about 9 m²?
The reservoir has the shape of a sphere with a diameter of 14 m. a) How many hectoliters (hl) of water can it hold? b) How many kg of paint is needed to paint the reservoir if it is painted three times and one kg of paint is enough to paint about 9 m²? - Ball screen
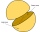 The diameter of the ball screen is 30 cm. If we add 5% of the material to be sewn, how many m² of fabric do we need to make?
The diameter of the ball screen is 30 cm. If we add 5% of the material to be sewn, how many m² of fabric do we need to make? - Balls
 Three metal balls with volumes V1=12 cm3, V2=112 cm3, and V3=59 cm³ were melted into one ball. Determine its surface area.
Three metal balls with volumes V1=12 cm3, V2=112 cm3, and V3=59 cm³ were melted into one ball. Determine its surface area. - Kilograms 7828
 The gas tank is a sphere with a diameter of 17.8 m. How many cubic meters of gas can it hold? If 1 kg of paint is enough to paint about 6 square meters, how many kilograms of paint are needed to paint a gas tank?
The gas tank is a sphere with a diameter of 17.8 m. How many cubic meters of gas can it hold? If 1 kg of paint is enough to paint about 6 square meters, how many kilograms of paint are needed to paint a gas tank? - Martians
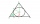 A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal?
A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal? - Tropics and polar zones
 What percentage of the Earth's surface lies in the tropical, temperate, and polar zones? Tropics border individual zones at 23°27' and polar circles at 66°33'.
What percentage of the Earth's surface lies in the tropical, temperate, and polar zones? Tropics border individual zones at 23°27' and polar circles at 66°33'. - A plane vs. sphere
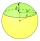 The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
