Triangle practice problems - page 3 of 126
Number of problems found: 2501
- A radio antenna
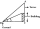 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Tower + pole
 On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole.
On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole. - An electrician 7
 An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal?
An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal? - Two men 2
 Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men.
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men. - Angle of elevation 3
 The angle of elevation of a pole from a point on the horizontal ground is 15°. After going up a distance of 10m towards the pole the angle of elevation became 30°.What is the height of the pole?
The angle of elevation of a pole from a point on the horizontal ground is 15°. After going up a distance of 10m towards the pole the angle of elevation became 30°.What is the height of the pole? - A kite 3
 A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th - Angle of elevation
 From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th - Elevation angle
 A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - The shadow 2
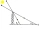 The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower. - The angle 9
 The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower - Angle of elevation
 The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters?
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters? - General right triangle
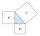 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - Triangle 97
 Triangle DEF with Ê=40°, F=90° EF = 45mm. Measure DE.
Triangle DEF with Ê=40°, F=90° EF = 45mm. Measure DE. - A right
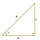 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - The hypotenuse
 The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides is 4 meters, find the other sides.
The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides is 4 meters, find the other sides. - Know one angle
 In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees. - The supplement
 The supplement of an angle is four times its complement. Find the angle.
The supplement of an angle is four times its complement. Find the angle. - Triangle 90
 Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make?
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - Angle of inclination
 Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long.
Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long. - A baseball
 A baseball is hit over the 325 foot fence, which is 110 feet tall. How far did the ball carry on a straight line when it reached the fence?
A baseball is hit over the 325 foot fence, which is 110 feet tall. How far did the ball carry on a straight line when it reached the fence?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
