Triangle practice problems - page 124 of 125
Number of problems found: 2494
- Flakes
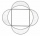A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Tetrahedral pyramid
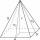What is the surface of a regular tetrahedral (four-sided) pyramid if the base edge a=16 and height v=16? - Circle annulus
There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have? - Arc and segment
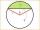Calculate the length of circular arc l, the area of the circular arc S1, and the area of circular segment S2. The circle's radius is 88, and the corresponding angle is (4)/(7) π. - Parallelogram - diagonals
Suppose a parallelogram ABCD, the length of one of its diagonals is equal to that of one of its sides. What are the interior angles of this parallelogram? - Pavement
Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m. - Parallelogram diagonals
Find the area of a parallelogram if the diagonals u1 = 15 cm and u2 = 12 cm and the angle formed by them is 30 degrees. - Equation of circle 2
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x. - The circle arc
Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m. - Quadrilateral prism
Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated? - Circumscribed hexa prism
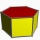The regular hexagonal prism is 2 cm high. The radius of the circle circumscribed by the base is 8 cm. Determine its volume and surface. - Circular segment
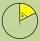Calculate the area of a circular segment if the radius r = 80 cm and the central angle is α = 110°. - Cone A2V
The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone. - Circular ring
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form. - Maximum of volume
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum? - Circle in rhombus
An inscribed circle is in the rhombus. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle's area. - The chord - angle
The distance of the chord from the center is 6 cm. The central angle is 60°. Calculate the area of the circular segment. - Concentric circles
In the circle with diameter, 13 cm is constructed chord 1 cm long. Calculate the radius of a concentric circle that touches this chord. - Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Line segments
Triangle ABC is divided by line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the area of quadrilateral AFHD.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
