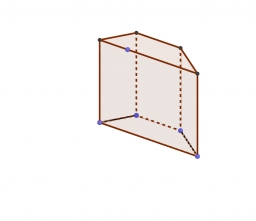
Quadrilateral prism

Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated?

Final Answer:

V =  1050 cm³
S =  769.4102 cm²

Step-by-step explanation:

$$\begin{gathered} a=10\text{cm} \\ c=4\text{cm} \\ v=6\text{cm} \\ h=25\text{cm} \\ {S}_1=\frac{a+c}{2}\cdot v=\frac{10+4}{2}\cdot 6=42{\text{cm}}^2 \\ V=S_1\cdot h=42\cdot 25=1050{\text{cm}}^3 \end{gathered}$$

$$\begin{gathered} x=\frac{a-c}{2}=\frac{10-4}{2}=3\text{cm} \\ r=\sqrt{x^2+v^2}=\sqrt{3^2+6^2}=3\sqrt{5}\text{cm}\doteq 6.7082\text{cm} \\ o=a+c+2\cdot r=10+4+2\cdot 6.7082\doteq 27.4164\text{cm} \\ {S}_2=o\cdot h=27.4164\cdot 25\doteq 685.4102{\text{cm}}^2 \\ S=2\cdot S_1+S_2=2\cdot 42+685.4102=769.4102{\text{cm}}^2 \end{gathered}$$

Try another example