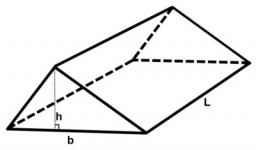
Triangular prism
Calculate the volume and surface of the triangular prism ABCDEF with base of a isosceles triangle. Base's height is 16 cm, leg 10 cm, base height vc = 6 cm. The prism height is 9 cm.
Correct answer:
Tips to related online calculators
Tip: Our volume units converter will help you with the conversion of volume units.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Triangular prism
Calculate the volume of a triangular prism 10 cm high, the base of which is an equilateral triangle with dimensions a = 5 cm and height va = 4,3 cm - Triangular prism
The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The content area of the largest sidewall of its surface is 130 cm², and the height of the body is 10 cm. Calculate its volume. - Triangular prism
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism. - Triangular prism
Calculate a triangular prism if it has a rectangular triangle base with a = 4cm and hypotenuse c = 50mm and height of the prism is 0.12 dm. - Prism
Calculate the surface area and volume of a prism with a body height h = 10 cm, and its base has the shape of a rhomboid with sides a = 5.8 cm, b = 3 cm, and the distance of its two longer sides is w = 2.4 cm. - Hexagonal prism
The base of the prism is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism. - Triangular prism
Calculate the surface of a triangular prism 10 cm high, the base of which is a triangle with sides 6 cm 8 cm, and 8 cm - Prism height
What is the prism's height with the base of a right triangle of 6 cm and 9 cm? The diaphragm is 10.8 cm long. The volume of the prism is 58 cm³. Calculate its surface. - Quadrangular prism
The quadrangular prism has a volume of 648 cm³. Trapezoid which is its base has the dimensions bases: a = 10 cm, c = 5 and height v = 6 cm. What is the height of the prism? - Find the
Find the volume and surface of a prism with a height of 120 mm, the base of which is an right isosceles triangle with a leg length of 5 cm. - The regular
The regular triangular prism has a base in the shape of an isosceles triangle with a base of 86 mm and 6.4 cm arms, the height of the prism is 24 cm. Calculate its volume. - Triangular prism
Calculate the volume and surface area of a triangular prism if it is given: a = 6.8 dm. ..Va = 4 dm. (base edge length and base triangle height length) ... ... .v = 23 dm (body height) - Triangular prism - regular
The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism. - Hexagonal prism
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - Triangular prism
Calculate the surface of a regular triangular prism, the edges of the base are 6 cm long and the height of the prism is 15 cm. - Regular triangular prism
Calculate the surface area of body of regular triangular prism, when the length of its base edge is 6.5 cm and height 0.2 m. - Triangular prism
The perpendicular triangular prism is a right triangle with a 5 cm leg. The content of the prism's largest wall is 130 cm2, and the body height is 10 cm. Calculate the body volume.
