Triangle practice problems - page 123 of 125
Number of problems found: 2498
- Pendulum
 Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm.
Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm. - Prism + rhomboid
 The prism-shaped vessel with a rhomboid base has one base diagonal of 10 cm and the edge of the base 14 cm. The edge of the base and the prism height are in a ratio of 2:5. How many liters of water is in the container when it is filled to four-fifths of t
The prism-shaped vessel with a rhomboid base has one base diagonal of 10 cm and the edge of the base 14 cm. The edge of the base and the prism height are in a ratio of 2:5. How many liters of water is in the container when it is filled to four-fifths of t - Diameter 5668
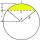 The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle?
The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle? - Chord
 It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB.
It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Truncated pyramid
 The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base. - Equilateral triangle v3
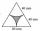 Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle.
Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle. - Determine 8010
 Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =? - Colored area
 How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Chord circle
 The circle to the (S, r = 8 cm) are different points A, B connected segment /AB/ = 12 cm. AB mark the middle of S'. Calculate |SS'|. Make the sketch.
The circle to the (S, r = 8 cm) are different points A, B connected segment /AB/ = 12 cm. AB mark the middle of S'. Calculate |SS'|. Make the sketch. - Quarter circle
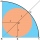 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm? - 4side pyramid
 Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees.
Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees. - Surface of the cone
 Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³.
Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³. - Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - Circle and chord
 The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc?
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Spherical segment
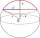 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm. - Quadrilateral prism
 The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism? - Parallelogram
 Find the parallelogram's perimeter, where base a = 8 cm, height v = 3 cm, and angle alpha = 35° is the magnitude of the angle at vertex A.
Find the parallelogram's perimeter, where base a = 8 cm, height v = 3 cm, and angle alpha = 35° is the magnitude of the angle at vertex A. - Square equal rhombus
 Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°.
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°. - A cell tower
 A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal?
A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
