Flakes
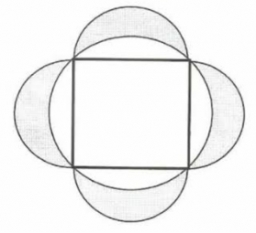
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips.
Which is bigger: the area of the middle square or the area of the four chips?
Which is bigger: the area of the middle square or the area of the four chips?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- comparing
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
- square
- circular sector
- circular arc
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Coat of arms
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo - The amphitheater
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Semicircle
The semicircle with center S and the diameter AB is constructed equilateral triangle SBC. What is the magnitude of the angle ∠SAC? - Determine 2860
Five natural numbers are given, each of which is a triple of the previous one. The largest number is bigger by 1152 than the middle number in this series. From these five numbers, determine the first number.
- What is bigger?
Which ball has a larger volume: a football with a circumference of 66 cm or a volleyball with a diameter of 20 cm? - Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Cutting square
We cut the circle with the highest possible diameter from a square with a side of 30 cm. How many percent of the square area is this circle?
