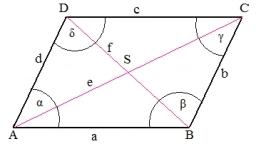
Parallelogram - diagonals

Suppose a parallelogram ABCD, the length of one of its diagonals is equal to that of one of its sides. What are the interior angles of this parallelogram?

Final Answer:

α =  120 °
β =  60 °
γ =  120 °
δ =  60 °

Step-by-step explanation:

$$\begin{gathered} \cos \beta =\frac{a}{2a}=\frac{1}{2} \\ \beta =\arccos (\frac{1}{2}) \\ \beta =60{}^{\circ } \\ \alpha =180-\beta =180-60=120^{\circ } \end{gathered}$$

$\gamma =\alpha =120=120^{\circ }$

$\delta =\beta =60=60^{\circ }$

Try another example