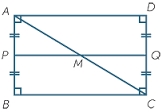
Construct diagonals
The point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of the rectangle ABCD.
Correct answer:
You need to know the following knowledge to solve this word math problem:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Square side
Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0. - Construct 10921
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Construct 11511
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options
- Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Square ABCD
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4]. - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
