Equation of circle 2
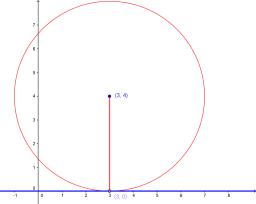
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x.
Result
Result
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle
Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r² - Integer
Find the integer whose distance on the numerical axis from number 1 is two times smaller than the distance from number 6. - A tree 2
A tree is broken at a height of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree . Find the original height of the tree. - Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
- Equation of circle
Find an equation of the circle with indicated properties: a. center at (-3,5), diameter 20. b. center at origin and diameter 16. - Intercept with axis
F(x)=log(x+4)-2, what is the x intercept - The frame
Rodney has a board that is 5/6 yards long. He cuts 1/5 yard off the board and uses the rest to make a frame. How much of the board is used to make the frame?
