Circle
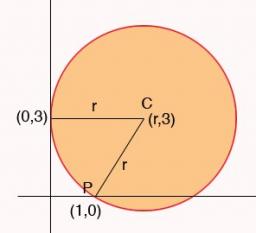
Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]:
(x−xS)2+(y−yS)2=r2
(x−xS)2+(y−yS)2=r2
Correct answer:
Tips for related online calculators
Do you have a system of equations and are looking for calculator system of linear equations?
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle - analytics geometry
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - General line equations
In all examples, write the GENERAL EQUATION OF a line that is given in some way. A) the line is given parametrically: x = - 4 + 2p, y = 2 - 3p B) the slope form gives the line: y = 3x - 1 C) the line is given by two points: A [3; -3], B [-5; 2] D) the lin - Perpendicular 82994
The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis. - Determine 82394 Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t,
- Coefficient 81704
In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4. - Line
Write an equation of a line parallel to To 9x + 3y = 8 That Passes Through The Point (-1, -4). Write in the form ax+by=c. - Prove
Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
