Unit conversion + similarity of triangles - practice problems
Number of problems found: 26
- Scale model
In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38? - Triangle-shaped 30011
Determine the map's scale if the 1.6 km, 2.4 km, and 2.7 km triangle-shaped forests are drawn on the map as a triangle with sides of 32 mm, 48 mm, and 54 mm. - Similarity 80742
Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm. - Vertical rod
The vertical one-meter-long rod casts a shadow 150 cm long. Calculate the height of a column whose shadow is 36 m long simultaneously.
- Chimney and tree Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long.
- Determine 82470
The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building. - Triangle 28611
The land has a triangle shape with sides of 300m, 200m, and 245m. Draw it on a scale of 1:5,000. - Similarity 26441
How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity. - Calculate 64444
The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden.
- The straight
The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m? - Calculate 5148
At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the river - Shadow of tree
Miro stands under a tree and watches its shadow and shadow of the tree. Miro is 180 cm tall, and its shade is 1.5 m long. The tree's shadow is three times as long as Miro's shadow. How tall is the tree in meters? - Mirror
How far must Paul place a mirror to see the top of the tower 12 m high? The height of Paul's eyes above the horizontal plane is 160 cm, and Paul is from the tower distance of 20 m. - Mast angles and height
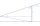Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
- Thales
Thales is 1 m from the hole. The eyes are 150 cm above the ground and look into the hole with a diameter of 120 cm, as shown. Calculate the depth of the hole. - Inclined plane
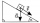The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body. - The chimney
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Tree shadow
The tree perpendicular to the horizontal surface has a shadow 8.32 meters long. At the same time, a one-meter rod perpendicular to the horizontal surface has a shadow 64 cm long. How tall is the tree? - Height of poplar
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar.
Peter is looking at John over a ruler that keeps at an arm's distance of 60 cm from the eye, and on the ruler, John measured the height of 15 mm. John is 2 meters high. How far from Peter stands John?Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
