Right triangle + similarity of triangles - practice problems
Number of problems found: 68
- Lighthouse
 The man, 180 cm tall, walks along the seafront directly to the lighthouse. The male shadow caused by the beacon light is initially 5.4 meters long. When the man approaches the lighthouse by 90 meters, its shadow is shorter by 3 meters. How tall is the lig
The man, 180 cm tall, walks along the seafront directly to the lighthouse. The male shadow caused by the beacon light is initially 5.4 meters long. When the man approaches the lighthouse by 90 meters, its shadow is shorter by 3 meters. How tall is the lig - Equilateral triangle ABC
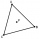 In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - Euclid theorems
 Calculate the sides of a right triangle if leg a = 6 cm and a section of the hypotenuse, which is located adjacent to the second leg b, is 5cm.
Calculate the sides of a right triangle if leg a = 6 cm and a section of the hypotenuse, which is located adjacent to the second leg b, is 5cm. - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence.
- Lighthouse
 Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s
Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s - Tower's view
 From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church.
From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church. - Rectangular triangles
 The lengths of corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and 8 c
The lengths of corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and 8 c - An observer
 An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower?
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - Isosceles 6673
 Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long.
Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long.
- Climb
 The road sign which informs the climb is 8.7%—the car drive 5 km along this road. What is the height difference that the car went?
The road sign which informs the climb is 8.7%—the car drive 5 km along this road. What is the height difference that the car went? - Display case
 Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs.
Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs. - Triangle KLB
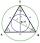 It is given equilateral triangle ABC. From point L, the midpoint of the side BC of the triangle, it is drawn perpendicular to the side AB. The intersection of the perpendicular and the side AB is point K. How many percents of the area of the triangle ABC
It is given equilateral triangle ABC. From point L, the midpoint of the side BC of the triangle, it is drawn perpendicular to the side AB. The intersection of the perpendicular and the side AB is point K. How many percents of the area of the triangle ABC - Isosceles 7661
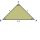 The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles.
The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles. - Shadow 73354
 How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long?
How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long?
- Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Determine 70834
 At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney.
At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney. - Shadows
 At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow? - A boy
 A boy of height 1.7m is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff.
A boy of height 1.7m is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - Boat
 A force of 300 kg (3000 N) is required to pull a boat up a ramp inclined at 14° with horizontal. How much does the boat weigh?
A force of 300 kg (3000 N) is required to pull a boat up a ramp inclined at 14° with horizontal. How much does the boat weigh?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
See also our right triangle calculator. See also our trigonometric triangle calculator. Right triangle practice problems. Similarity of triangles - practice problems.
