Volume - math word problems - page 30 of 126
Number of problems found: 2516
- Remaining side
Calculate the remaining side of the rectangle when you know the size of the perimeter and the length of one side. Perimeter o=38cm, and side a=12cm. - Trapezoid 65644
In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm². - Processing 65514
The Nováková family took a loan (loan) of 120,000 euros from the bank. What was the amount of the fee for processing, setting up, and providing the loan if, according to the bank's fee schedule, it is 0.80% of the loan volume, but at least 250 euros and a - Material 65504
The cube with an edge of 1 cm weighs 0.2 kg. What is the weight of a cube made of the same material with an edge 4 cm long? - Measuring 65374
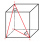Calculate the length of the body diagonal of a block measuring 6 cm, 7 cm, and 10 cm, and round the result to two decimal places. - Calculate sphere cap
Calculate the surface of a spherical cap with a height of 6 cm and a radius of 15 cm - Calculate 65154
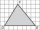Each square of the net has an area of 25 mm². Calculate the area of the DEF triangle in cm². Express the result as a decimal number to three decimal places. - Dimensions: 65144
Calculate the volume of the block in dm³ S dimensions: a = 22cm b = 80dm c = 0.63m - Substantial 65114
Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm. - Dimensions 65094
The whirlpool has external dimensions of 2.29, 2.29 m, and 91 cm. The useful volume of water in it is 1514 liters. What volume of the whirlpool falls on the other parts? - Cube-shaped 65084 The cube-shaped container can hold precisely 8 cm³ of bath salt. How many cm³ of bath salt will fit in a cube-shaped container with an edge twice as long?
- Bricklayer 65064
The bricklayer could repair the wall himself in 30 minutes. Students would learn in an hour. How long will it take them to work together? - Gasoline 65034
My father refueled 40 liters of gasoline for 61.40 euros. He then refueled 8 liters of the same petrol into an empty canister. How many euros did gasoline cost in a canister? - Calculate 65014
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string? - Circumference 64994
Calculate the volume of the cylinder if the circumference of the base o = 31.4 cm, height v = 6.4 cm - Calculate: 64984
The ABCDEFGH cube (sketch it) has a debt edge of 5 cm. Calculate: a) ABFE wall area b) Area of the ADHE wall c) the surface of the cube d) Cube volume - Perimeter 64974
The prism has a square base with an edge 5 cm long and 20 cm high. Calculate it: (a) the area of the base b) the perimeter of the base c) volume d) surface - Dimensions 64944
The swimming pool's interior, with dimensions of 50m, 15m, and 3m, should be lined with tiles. How many square meters of tiles are used for this? - Approximately 64934
How many kg of paint will we use to paint the walls and ceiling of a room with a length of 9m, a width of 6m, and a height of 3.2m if 1kg of paint is enough for approximately 6m square? Subtract 6 square meters from the surface of the walls, which are the - Difference 64924 We get a block if we stack two cubes with an edge of 1dm. What is the difference between the surfaces of this block and the cube?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
