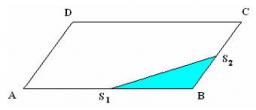
Parallelogram ABCD
The area of parallelogram ABCD is 906 cm2. Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND?
Final Answer:
Showing 1 comment:
Ken
The area of parallelogram ABCD is 440 cm2. Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND? A solution would help
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Equilateral 4301
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF? - Smaller square
Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD? - Quadrilateral 81097
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Parallelogram ABCD
We have the parallelogram ABCD, where AB is 6.2 cm; BC is 5.4 cm and AC is 4.8 cm. Calculate the height on the AB side and the angle DAB. - Circumference 3088
In the parallelogram ABCD, the side AB is three times longer than the side BC. The circumference of the parallelogram is 20 cm. Find the lengths of the sides of the parallelogram. - Rectangle - parallelogram
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Parallelogram - angle alfa In the parallelogram ABCD the length of sides are AB = 8, BC = 5, BD = 7. Calculate the magnitude of the angle α = ∠DAB (in degrees).
