Three points
Mark three points E, F, and G in the plane, not lie on one line.
a) Draw a line segment FG
b) Construct halfline (ray) EG
c) Draw a line EF
a) Draw a line segment FG
b) Construct halfline (ray) EG
c) Draw a line EF
Final Answer:

You need to know the following knowledge to solve this word math problem:
geometrythemes, topicsGrade of the word problem
Related math problems and questions:
- Distance 15203
 In the plane, the points A, B, and C are given 3 cm apart, and they do not lie in the same straight line. Mark the set of all points whose distance from all three points is less than or equal to 2.5 cm.
In the plane, the points A, B, and C are given 3 cm apart, and they do not lie in the same straight line. Mark the set of all points whose distance from all three points is less than or equal to 2.5 cm. - Connect 6500
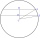 Draw the line KL = 55mm. Draw a circle k with center K and a radius of 4cm. Mark the points to belong to the circle and connect them with point L.
Draw the line KL = 55mm. Draw a circle k with center K and a radius of 4cm. Mark the points to belong to the circle and connect them with point L. - MO - triangles
 On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Draw it!
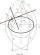 Draw two lines c, d that c || d. On line c, mark points A and B. By point A, a lead perpendicular line to c. By point B, lead perpendicular line to c.
Draw two lines c, d that c || d. On line c, mark points A and B. By point A, a lead perpendicular line to c. By point B, lead perpendicular line to c. - Diagonals 14073
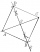 There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you
There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you - Points in space
 There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points?
There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points? - Rhombus construct
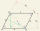 Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
