Series and sequences
Find a fraction equivalent to the recurring decimal.
0.435643564356
0.435643564356
Final Answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticnumbersGrade of the word problem
Related math problems and questions:
- Identify 4
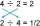 Identify the whole number whose reciprocal has a decimal equivalent between 0.2 and 0.3. Explain.
Identify the whole number whose reciprocal has a decimal equivalent between 0.2 and 0.3. Explain. - Lila knows
 Lila knows that 3/16 means "3 divided by 16." She uses this to find the decimal equivalent for 3/16. Enter a digit into each box to continue her work.
Lila knows that 3/16 means "3 divided by 16." She uses this to find the decimal equivalent for 3/16. Enter a digit into each box to continue her work. - Decimal to fraction
 What is 0.99 into a fraction?
What is 0.99 into a fraction? - Which 11
 Which decimal is equivalent to 5/6
Which decimal is equivalent to 5/6 - Decimal equivalent
 Which mixed number is equivalent to 2.68? A:2 and 6-eighths B:2 and 68-tenths C:2 and 6 over 68
Which mixed number is equivalent to 2.68? A:2 and 6-eighths B:2 and 68-tenths C:2 and 6 over 68 - Equivalent fractions 3
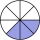 What fraction is equivalent to 1/3? Write three equivalent fractions to 1/3.
What fraction is equivalent to 1/3? Write three equivalent fractions to 1/3. - 2/3 write
 2/3 write it in an equivalent decimal
2/3 write it in an equivalent decimal
