Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
Final Answer:
Showing 2 comments:
Dr Math
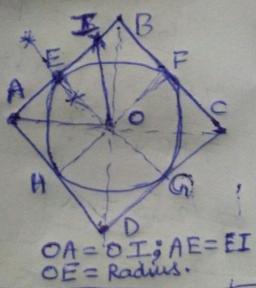
1. draw line segment AB = 6 cm
2. draw circle k1 (B, r=6 cm)
2. draw circle k2 (A, r=9 cm)
4. point C is intersect k1 and k2
5. draw line u2 from B perpendicular to AC
6. draw circle k3 (A, r=6 cm)
7. point D is intersect k3 and line u2
8. connect points ABCD to rhombus
9. point S is intersect of AC diagonal and BD diagonal
10. make perpendicular line u3 from S to AB.
11. draw inswribed circle with center S and radius SX, X is intersection of u3 and AB
2. draw circle k1 (B, r=6 cm)
2. draw circle k2 (A, r=9 cm)
4. point C is intersect k1 and k2
5. draw line u2 from B perpendicular to AC
6. draw circle k3 (A, r=6 cm)
7. point D is intersect k3 and line u2
8. connect points ABCD to rhombus
9. point S is intersect of AC diagonal and BD diagonal
10. make perpendicular line u3 from S to AB.
11. draw inswribed circle with center S and radius SX, X is intersection of u3 and AB
Dr Math
another steps:
1. Draw AC = 9cm horizontally.
2. With A as center and AB =6cm as radius, draw arcs above and below AC.
3. With C as center and AB as radius, draw arcs to cut the earlier arcs.
4. Intersection points are B and D.
5. Join all sides.
6. Draw BD. The intersection of AC AND BD is O , the center of the incircle.
7. Draw an arc with O as center and OB as radius to cut BC at E.
8. Draw perpendicular bisector of BE. It passes through O. Mid point of BE is F.
9. OF as radius and O as center draw the incircle.
1. Draw AC = 9cm horizontally.
2. With A as center and AB =6cm as radius, draw arcs above and below AC.
3. With C as center and AB as radius, draw arcs to cut the earlier arcs.
4. Intersection points are B and D.
5. Join all sides.
6. Draw BD. The intersection of AC AND BD is O , the center of the incircle.
7. Draw an arc with O as center and OB as radius to cut BC at E.
8. Draw perpendicular bisector of BE. It passes through O. Mid point of BE is F.
9. OF as radius and O as center draw the incircle.
You need to know the following knowledge to solve this word math problem:
planimetricsthemes, topicsGrade of the word problem
Related math problems and questions:
- Construct 5333
 Construct a rhombus ABCD if AB = 5 cm, BD = 6 cm and AC = 3 cm
Construct a rhombus ABCD if AB = 5 cm, BD = 6 cm and AC = 3 cm - Construct rhombus
 Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm
Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm - Construct 80719
 Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle.
Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle. - Rhombus construct
 Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Construct
 Construct a rhombus ABCD if the size of the diagonal AC is 6 cm and the diagonal BD is 8 cm long.
Construct a rhombus ABCD if the size of the diagonal AC is 6 cm and the diagonal BD is 8 cm long. - Triangle in a square
 In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides.
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Rectangle and diagonal
 In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area.
In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area.
