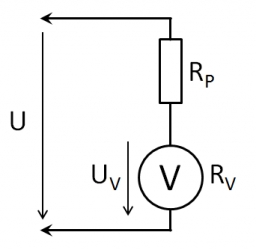
Voltmeter range
We have a voltmeter which, in the original set, measures voltage to 10V. Calculate the size of the ballast resistor for this voltmeter if we want to measure the voltage up to 50V. Voltmeter's internal resistance is 2 kiloohm/Volt.
Correct answer:
You need to know the following knowledge to solve this word math problem:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Effective and mean voltage
A voltage divider consisting of resistors R1 = 103000 Ω and R2 = 197000 Ω is connected to the ideal sine wave voltage source. R2 is connected to a voltmeter, which measures the mean voltage and has an internal resistance R3 = 200300 Ω. The measured value - Scale of voltmeter
Which scale division (scale has 100 divisions) must the voltmeter hand point at a measuring range of 300V if we want to measure a voltage of 100V? - Individual 46993
We measured the voltage U= 75 V between the circuit's external terminals with a voltmeter. The circuit's resistance values of the individual resistors (in series) are 50 Ohm and 100 Ohm. Find out what voltage we would measure on the 1st and 2nd resistor - Resistance 25031
The current of 25 mA passes through the resistor with a resistance of 50Ω. How much voltage do we measure on it?
- Resistance 18883
A current of 20mA passes through the resistor, which is connected to a voltage of 2.5V. What is the resistance of the resistor? - Electrical 19373 At a certain point, we measured a voltage of 3.74V at a current of 170mA at the terminals of a resistor connected to an electrical circuit. Calculate the resistance of the resistor.
- Serial resistors
In the circuit shown ( two resistors, R1 and R2, serially connected), the total resistance from A to B is 16 ohms. If the voltage between A and B is 10 V, find the resistance R2 and the current through the R1 = 12-ohm resistor.
