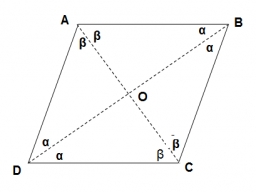
A rhombus
A rhombus has sides of the length of 10 cm, and the angle between two adjacent sides is 76 degrees. Find the length of the longer diagonal of the rhombus.
Final Answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Rhombus
The rhombus with area 95 has one diagonal that is longer by 7 than the second one. Calculate the length of the diagonals and rhombus sides. - Circumference 26361
The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond. - Cuboid diagonal
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees. - Degrees 70334
What is the height of a diamond with a side 6 cm long if the angle formed by the sides is 78 degrees and 10 '? - Rhombus
One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus. - Perpendicular sides
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ - A rectangle 5
A rectangle has sides of 10 cm and 14 cm. Calculate the angle between a diagonal and a long side.
