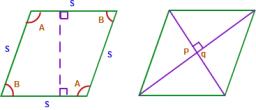
Rhombus
One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- One of
One of the internal angles of the rhombus is 120°, and the shorter diagonal is 3.4 meters long. Find the perimeter of the rhombus. - A rhombus 4
A rhombus has a side length of 10 cm. Find the angles at each vertex of the rhombus if the shorter diagonal measures 7 cm. Give your answers to the nearest degree and provide clear geometric reasoning at each step. - Rhombus 47
A rhombus has a side length of 5 m and a longer diagonal of 8 m. What is the length of the shorter diagonal? - Rhombus
Internal angles of a rhombus are in the ratio 2:5. How many times is the shorter diagonal longer than the side of the rhombus? - Diagonal
The diagonal of the rectangle has a length of 39.5 cm. The angle between the diagonal and longer side of the rectangle is 43°. Calculate the area of the rectangle. - The area
The area of a rhombus is 143 m². If the longer diagonal is 26 m, find the shorter diagonal in inches named d1. - Rhombus 36 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
