Cylinder - A&V
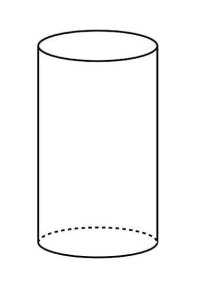
A cylinder has a volume of 463. Its base has a radius of 4. What is the total surface area of the cylinder?
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Diameter 132
The base diameter of a cylinder is 2 m and its total surface area is 34.54 m². Calculate the base radius, height, and volume of the cylinder. - Cylinder surface area
The volume of a cylinder whose height is equal to the radius of the base is 678.5 dm³. Calculate its surface area. - Cylinder - basics
A cylinder has a base radius r = 24 cm and height h = 62 cm. Calculate: a) The area of the base - Cylinder height surface
The volume of the cylinder is 193 cm³, and the radius of its base is 6.4 cm. Calculate the height and surface of the cylinder to 1 decimal place. - The surface
The surface of the cylinder is 1570 cm²; its height is 15 cm. Find the volume and radius of the base. - Rotary cylinder 2 The base circumference of the rotary cylinder has the same length as its height. What is the surface area of the cylinder if its volume is 250 dm³?
- Cylinder The cylinder surface is 922 dm². Its height is equal to the radius of the base. Calculate the height of this cylinder.
