Triangle midpoints
Determine coordinates of triangle ABC vertices if we know triangle sides midpoints SAB [0;3] SBC [1;6] SAC [4;5], its sides AB, BC, AC.
Correct answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
Do you have a system of equations and are looking for calculator system of linear equations?
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
Do you have a system of equations and are looking for calculator system of linear equations?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Coordinates 32183
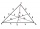The triangle ABC is given in the plane. A (-3,5), B (2,3), C (-1, -2) write the coordinates of the vectors u, v, w if u = AB, v = AC, and w = BC. Enter the coordinates of the centers of the lines SAB (..), SAC (...), SBC (. ..) - Intersection 81611
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides. - Calculate 82578
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Equilateral 4301
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF?
- Grassland and goat
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is - Triangle 3552
Draw a circle k (S, r = 3cm). Build a triangle ABC so that its vertices lie on the circle k and the length of the sides is (AB) = 2.5 cm (AC) = 4 cm - Segment
Calculate the segment AB's length if the coordinates of the end vertices are A[0, -2] and B[-4, 9].
