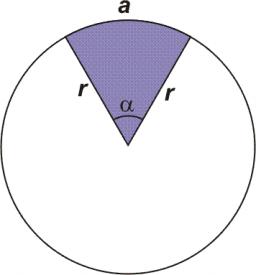
Circular sector

I have a circular sector with a length 15 cm with an unknown central angle. It is inscribed by a circle with radius 5 cm. What is the central angle alpha in the circular sector?

Your answer:

°


Did you find an error or inaccuracy? Feel free to write us. Thank you!



avatar




Tips to related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:


 
We encourage you to watch this tutorial video on this math problem: video1