Geometric mean
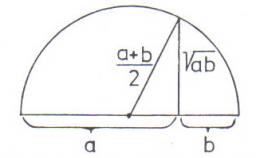
Calculate the geometric mean of numbers a=15.2 and b=25.6. Determine the mean by construction where a and b are the length of the lines.
Correct answer:
Tips for related online calculators
Looking for a statistical calculator?
You need to know the following knowledge to solve this word math problem:
statisticsalgebraarithmeticnumbersGrade of the word problem
Related math problems and questions:
- Quotient
Determine the quotient and the second member of the geometric progression where a3=10, a1+a2=-1.6, and a1-a2=2.4. - Midpoint of the line segment
Length of lines MG = 7x-15 and FG = 33 Point M is the midpoint of FG. Find the unknown x. - Variance and average
Of the 40 values were calculated average mx = 7.5 and variance sx = 2.25. After we found the control to lack the two items of the values of x41 = 3.8 and x42=7. Correct the above characteristics (mx and sx). - Probabilities 71194
We have a dummy die where numbers fall with probabilities P (1)=0.1; P (2)=0.2; P (3)=0.22; P (4)=0.16; P (5)=0.24; P (6)=0.08. Determine the probability that the two toss the same numbers.
- Intersection 3383
A regular 15-angle is given. A triangle is formed if we connect points 3 and 7, 13 and 10. The vertices are 3 and 13, and the lines' intersections are 3.7 and 13.10. We are to determine the angle size formed by sides 3.7 and 13.10. These numbers indicate - From MAN statistics
It was determined how many points from the homework assignments in statistics were received by randomly selected students of the MAN field and how many by randomly selected students of the THK field. It was found: MAN x/17/17/15/21/29/30/16/18/15/25/16/ T - Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati
