Cone roof

How many m² of roofing is needed to cover a cone-shaped roof with a diameter of 10 m and a height of 4 m? Add an extra 4% to the overlays.

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

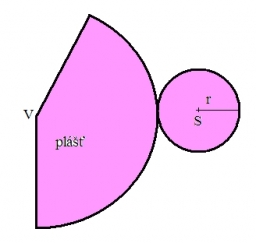
Tips for related online calculators

Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

solid geometry

cone
surface area

planimetry

Pythagorean theorem
right triangle
triangle

basic operations and concepts

percentages

Grade of the word problem

practice for 14 year olds
high school

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

Church roof 2
The roof has the shape of a rotating cone shell with a base diameter of 6 m and a height of 2.5 m. How much money (CZK) will cost the roof cover sheet if 1 m² of metal sheet costs 152 CZK and if you need 15% extra for joints, overlays, and waste?
Castle tower
The castle tower has a cone-shaped roof with a diameter of 10 meters and a height of 8 meters. If we add one-third to the overlap, calculate how many m² of coverage is needed to cover it.
Tower roof
The tower's roof is a cone with a base diameter of 12 m and a height of 8 m. At least how many square meters of roofing are needed to cover it?
Roof material
How many square meters of roofing is needed to cover the cone-shaped roof if the perimeter of its base is 15.7 m and a height of 30 dm
Calculation - hemisphere
The roof is shaped like a hemisphere with a diameter of 8 m. Calculate how much m² of roofing is needed to cover the entire top if we count 15% for waste and residues and round the result to tenths of m². Use the constant pi rounded to two decimal places
Cone roof cost
The roof of the castle tower has the shape of a cone with a base diameter of 12 m and a height of 8 m. How many euros will we pay to cover the roof if 1 m of square roofing costs 3.5 euros?
Pyramid-shaped roof
A block-shaped shed is covered with a quadrilateral pyramid-shaped roof with a base with sides of 6 m and 3 m and a height of 2.5 m. How many m² (square meters) must be purchased if an extra 40% is calculated for roofing and waste?