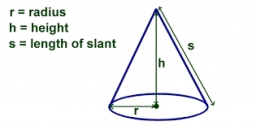
The conical
The conical candle has a base diameter of 20 cm and a side of 30 cm. How much dm3 of wax was needed to make it?
Correct answer:
Tips for related online calculators
Do you know the volume and unit volume, and want to convert volume units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Pyramidal 44061
A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height? - Wax candles
A company makes wax candles in the shape of a cylinder. Each candle has a diameter of 4 inches and a height of 7 inches. If the company used 7561.12 in³ of wax, how many candles did it make? Use 3.14, and do not round your answer. - Hexagonal wax
The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax. - Calculate 82409
The lamp shade should be formed by the shell of a cone with a base diameter of 48 cm and a side of 32 cm. Calculate how much material will be needed to make it, assuming 8% waste - Cone-shaped 23331
For his birthday, Jirka made a cone-shaped hat out of paper. The side of this cone is 35cm long, and the radius of its base is 20cm. How much dm of paper did Jirka use to make it? Thank you - Measuring 67734
The candle is shaped like a block measuring 3 cm, 4 cm, and 5 cm. If we gradually enlarge one, two, and all three edges twice, how many times is more wax used to make a candle? - Lampshade 7846
Lampshade for the face of a truncated cone with a height of 20 cm. The upper diameter of the shade is 13 cm, the lower 36 cm, and the side forms an angle of 60 degrees with the lower diameter. At least how much fabric is needed to make this shade?
