Dimensions 26713
A rectangle with dimensions of 11 x 13 pieces consists of 11*13 = 143 small identical squares. How many squares, made up of nine small squares, can be drawn in this rectangle (squares can overlap)?
Correct answer:
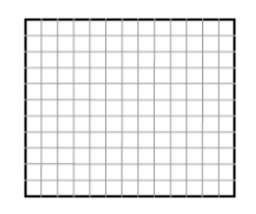
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- MO-Z5-3-66 tiles
The picture shows square tiles with a side of 10 dm, composed of four identical small rectangles and squares. The circumference of a small square is five times smaller than the circumference of the entire tile. Determine the dimensions of the rectangle. - Z6–I–5 MO 2019
The shape in the picture was created by cutting a small cross out of a large cross. Each of these crosses can be composed of five identical squares, with the sides of the small squares being half the sides of the large squares. The area of the gray shap - Dimensions 82501
The table has the shape of a rectangle with dimensions of 80 × 100 cm. Ten identical sheets of paper measuring 20 x 30 cm lie next to each other on it. Papers do not overlap or extend beyond the surface of the table. What part of the table surface is cove - Gardens colony
The garden's colony, with dimensions of 180 m and 300 m, is to be completely divided into the same large squares of the highest area. Calculate how many such squares can be obtained and determine the length of the square side.
- Dimensions 21153
The sheet of paper has the dimensions a = 28 cm and b = 8 cm. How many 4 cm squares can we cut from the paper? (draw a picture) - Tinsmith
Tinsmith constructs chimney pipe 186 cm long and 16 cm wide. A pipe is made from the plate overlap at the joint and needs to add $x cm width of the plate. What dimensions of the sheet will have to be prepared for the construction? - Square gardens
The gardening colony with dimensions of 180 m and 300 m is to be completely divided into equally large square areas with the largest possible area. Calculate how many such square areas can be obtained and determine the square's side length.
