Z6–I–5 MO 2019
The shape in the picture was created by cutting a small cross out of a large cross. Each of these crosses can be composed of five identical squares, with the sides of the small squares being half the sides of the large squares. The area of the gray shape in the picture is 45 cm2. What is the area of the large cross?
Final Answer:

You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cross five
 The figure in the picture is composed of the same squares and has an area of 45cm². What is its perimeter?
The figure in the picture is composed of the same squares and has an area of 45cm². What is its perimeter? - Coat of arms
 The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo - Resulting cross
 From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross?
From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross? - Identical cubes
 What is the volume of a large cube composed of 27 identical small cubes with an edge length of 3 cm?
What is the volume of a large cube composed of 27 identical small cubes with an edge length of 3 cm? - MO-Z5-3-66 tiles
 The picture shows square tiles with a side of 10 dm, composed of four identical small rectangles and squares. The circumference of a small square is five times smaller than the circumference of the entire tile. Determine the dimensions of the rectangle.
The picture shows square tiles with a side of 10 dm, composed of four identical small rectangles and squares. The circumference of a small square is five times smaller than the circumference of the entire tile. Determine the dimensions of the rectangle. - Rectangle square counting
 A rectangle with dimensions of 11 x 13 pieces consists of 11*13 = 143 small identical squares. How many squares, made up of nine small squares, can be drawn in this rectangle (squares can overlap)?
A rectangle with dimensions of 11 x 13 pieces consists of 11*13 = 143 small identical squares. How many squares, made up of nine small squares, can be drawn in this rectangle (squares can overlap)? - Cube corners
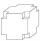 We cut a small cube with an edge length of 2 cm from each corner of a large cube with an edge length of 10 cm. How many cm³ was the body left from the big cube after cutting the small cubes?
We cut a small cube with an edge length of 2 cm from each corner of a large cube with an edge length of 10 cm. How many cm³ was the body left from the big cube after cutting the small cubes?
