Lamps on playground
The playground has the shape of a rectangle of 36 x 50 m. After how many meters can place the lamps on its lighting, if the distances between them are to be the same on both sides if the builders want to use the smallest possible number of lamps?
Your answer:
Your answer:
Tips for related online calculators
Do you want to calculate the least common multiple of two or more numbers?
Do you want to perform natural numbers division - find the quotient and remainder?
Do you want to perform natural numbers division - find the quotient and remainder?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetrynumbers
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Angles of elevation
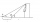From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37°, respectively. If |AB| = 57 m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side o - Playground
On the special playground, there are 81 square sectors, each with a side of 5 m. How many players can fit on the playground if each player needs a 75 m² area to play? - Book paper area
Approximately how many square meters of paper are needed to make a 500-page book that measures 29.7 cm by 21 cm (printed on both sides of the paper). - Lamp brightness
Ten lamps with a certain luminosity are needed to illuminate the rooms. How many lamps with 2.5 times more brightness are needed for the same lighting in the same room? - Playground Shorter Side
The playground has a rectangular shape. The length of the line around its perimeter is 440 m. The longer side of the course is 140 m long. How many meters does the size of the shorter side of the pitch measure? - Fence posts
Mr. John's plot of land has dimensions of 252 dm and 28 m. How far apart must he place the fence posts so they are the same distance on both sides? How many will he need to fence the entire property? - Two sides paint
The door is a rectangle with dimensions of 260 cm and 170 cm. How many cans of paint will be needed to paint this door if one can of paint cover 2 m² of the area? We paint the doors on both sides.
