Diofant equation
In the set of integers (Z), solve the equation:
212x+316y=0
Write result with integer parameter t∈Z (parameter t = ...-2,-1,0,1,2,3... if equation has infinitely many solutions)
212x+316y=0
Write result with integer parameter t∈Z (parameter t = ...-2,-1,0,1,2,3... if equation has infinitely many solutions)
Final Answer:
Tips for related online calculators
Do you want to calculate the greatest common divisor of two or more numbers?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
You need to know the following knowledge to solve this word math problem:
algebranumbersGrade of the word problem
Related math problems and questions:
- Root equation
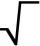We have 2 numbers. If we multiplied the first number's third root by the second number's square root, we would get the number 18. Determine these 2 numbers. Calculate only the integer solution if the problem has infinitely many solutions in the set of rea - Find x 2
Find x, y, and z such that x³+y³+z³=k for each k from 1 to 100. Write down the number of solutions. - Has infinity many solutions
Solve the equation and determine the type of solution the equation has. Select all possible answers. 6y+9=3(2y+3) - Equation
Solve the equation and check the result: 1.6x - 3/2 + x - 9,8 = x + 0,4/3 - 7 + 1,6/6 - Three equations
Solve the following set of equations with three unknowns. 3x + 2y + 3z = 110 5x-y-4z = 0 2x-3y + z = 0 - Solve 2
Solve integer equation: a +b+c =30 a, b, c = can be an odd natural number from this set (1,3,5,7,9,11,13,15) - Integer part system
In the field of real numbers, solve the system of equations: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ denotes the (lower) integer part of the real number a, i.e., the largest integer not greater than a., E.g., ⌊1.9⌋ = 1 and ⌊−1.1⌋ = −2.)
