Six terms GP
Find the sum of the six terms of the finite geometric sequence 96, -48, 24, -12
Correct answer:
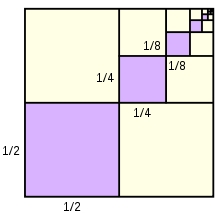
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- GP sequence
Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 5, an = 320, sn = 635, n =? q =? - Parabolic sequence
Find the sum of the first nine terms of an arithmetic sequence whose general term is a(n) = 3n²+5 - Six terms
Find the first six terms of the sequence a1 = -3, an = 2 * an-1 - Sum 1-6
Find the sum of the geometric progression 3, 15, 75,… to six terms.
- Finite geometric sequence Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =?
- Calculate 82845
Calculate the sum of the first 9 terms of the geometric sequence if a3 equals 2 and a4 equals 8. - GP - sequence
The first three terms of a geometric sequence are as follows: 10, 30, 90. Find the next two terms of this sequence.
