Harry
Harry Thomson bought a large land in the shape of a rectangle with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of equal length. Their longer sides are three consecutive natural numbers. Find out each plot's dimensions and the whole plot's area.
Correct answer:
Tips for related online calculators
Do you have a system of equations and are looking for calculator system of linear equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circumference 6382
Jan bought a large rectangle plot with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of the same length. Their longer sides are three consecutive natural numbers. Find out each plot's dimens - Rectangles
The perimeter of a rectangle is 90 m. Divide it into three rectangles. The shorter side has all three rectangles the same. Their longer sides are three consecutive natural numbers. What are the dimensions of each rectangle? - Rectangular 4184
The rectangular plot has sides 20m and 28m long. Calculate the area of the rhizome and find out how long the longer side of the plot with the same area must be if the shorter side is 16 meters long. Also, calculate the length of the fence around each rhiz - L gardens
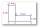Find how long the area with gardens is if the square plots have a circumference of 8 m and the rectangular plot has a circumference of 14 m. The gardens are adjacent so that the shorter side of the rectangular plot is adjacent to the first square garden,
- The land
The owner wants to divide the land with dimensions of 220 m and 308 m into equally large square plots with the largest possible area. How long will one side of the plot be? - Three gardens
Is it possible to divide a plot of land with an area of 927 m² into three gardens in a ratio of 4:2:3 so that their areas are only whole multiples of square meters? - Rectangular 82520
The sides of the rectangular forest plot are in the ratio 11:7. The shorter side of the plot is 175 meters long. Calculate the longer side of the rectangular plot. How many steps would we take if we went around the whole lot? The length of 1 step is 60 cm
