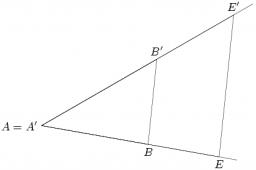
Two similar triangles
Find unknown sides of a similar triangles:
a = 6cm, b = 8cm, c =?,
a '=?, b '= 12cm, c' = 15cm
a = 6cm, b = 8cm, c =?,
a '=?, b '= 12cm, c' = 15cm
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Similar triangles
The triangles ABC and XYZ are similar. Find the unknown lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - Similar triangles
The triangles ABC and XYZ are similar. Find the unknown lengths of the sides of the triangles. The lengths: a = 5cm, b = 8cm and x = 7.5cm z = 9cm. - Similarity coefficient
Given triangle ABC with sides a = 12 cm b = 9 cm c = 7 cm and triangle DEF with sides d = 8.4 cm, e = 6.3 cm f = 4.9 cm Find out if triangles ABC and DEF are similar if so, write the similarity coefficient and according to which sentence they are similar - Similar triangles
In the triangle DEF is DE = 21cm, EF = 14.7cm, DF = 28cm. The triangle D'E'F' is similar to the triangle DEF. Calculate the lengths of the sides of the triangle D'E'F' if the similarity coefficient is one-seventh.
- Two similar
There are two similar triangles. One has a circumference of 100 cm, and the second has sides successively 8 cm, 14 cm, and 18 cm longer than the first. Find the lengths of its sides. - The triangles
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5 - Right-angled 40961
A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate the percentage of the area of triangle ABC that is the area of triangle A'B'C'.
