Similarity coefficient
In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other.
Final Answer:
Tips for related online calculators
Check out our ratio calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Similarity of two triangles
 The KLM triangle has a side length of k = 6.3cm, l = 8.1cm, m = 11.1cm. The triangle XYZ has a side length of x = 8.4cm, y = 10.8cm, z = 14.8cm. Are triangle KLM and XYZ similar? (write 0. If not, if yes, find and write the coefficient of a similarity)
The KLM triangle has a side length of k = 6.3cm, l = 8.1cm, m = 11.1cm. The triangle XYZ has a side length of x = 8.4cm, y = 10.8cm, z = 14.8cm. Are triangle KLM and XYZ similar? (write 0. If not, if yes, find and write the coefficient of a similarity) - Similar triangles
 In the triangle DEF is DE = 21cm, EF = 14.7cm, DF = 28cm. The triangle D'E'F' is similar to the triangle DEF. Calculate the lengths of the sides of the triangle D'E'F' if the similarity coefficient is one-seventh.
In the triangle DEF is DE = 21cm, EF = 14.7cm, DF = 28cm. The triangle D'E'F' is similar to the triangle DEF. Calculate the lengths of the sides of the triangle D'E'F' if the similarity coefficient is one-seventh. - Similar triangles
 The triangles ABC and XYZ are similar. Find the unknown lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm
The triangles ABC and XYZ are similar. Find the unknown lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - The triangles
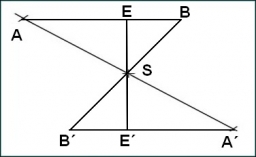
 Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5 - Similarity coefficient
 Given triangle ABC with sides a = 12 cm b = 9 cm c = 7 cm and triangle DEF with sides d = 8.4 cm, e = 6.3 cm f = 4.9 cm Find out if triangles ABC and DEF are similar if so, write the similarity coefficient and according to which sentence they are similar
Given triangle ABC with sides a = 12 cm b = 9 cm c = 7 cm and triangle DEF with sides d = 8.4 cm, e = 6.3 cm f = 4.9 cm Find out if triangles ABC and DEF are similar if so, write the similarity coefficient and according to which sentence they are similar - The triangles
 The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '.
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Triangle side
 The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm.
The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm.
