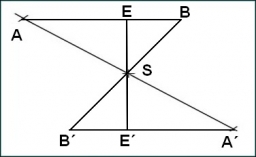
V trojuholniku 6
V trojuholníku tma platí, že dĺžka strán t =5cm, m =3,5cm, a=6,2cm . Iný s ním podobný trojuholník má dĺžky strán 6,65cm 11,78cm 9,5cm. Urč koeficient podobnosti týchto trojuholníkov. Priraď tieto dĺžky k stranám trojuholníka NOC, tak aby platilo TMA~NOC
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- V trojuholníku 7
V trojuholníku DEF je DE= 21cm, EF=14,7cm, DF=28cm. Trojuholník D´E´F´ je podobný s trojuholníkom DEF. Vypočítaj dlžky strán trojuholníka D´E´F´, ak koeficient podobnosti je jedna sedmina. - V trojuholníku
V trojuholníku ABC je [AB]=20cm, [BC]=10cm, A=30°. Zostroj trojuholník A'B'C' podobný s trojuholníkom ABC, ak koeficient podobnosti je 0,5 - Vypočítaj 376
Vypočítaj obvod trojuholníka ABC, ak vieš, že je podobný trojuholníku EFG, v ktorom e=144 mm, f=164 mm, g=92 mm a pomer podobnosti je 4. Výsledok vyjadri v cm. - Koeficient podobnosti 2
Trojuholníky ABC a A"B"C" sú podobné koeficientom podobnosti 2 . Veľkosti uhlov trojuholníka ABC sú α= 35° a β= 48°. Urči veľkosti všetkých uhlov trojuholníka A"B"C". - Podobnosť
Strany trojuholníka ABC majú dĺžky 4 cm, 5 cm a 7 cm. Zostroj trojuholník A'B'C' podobný trojuholníku ABC, ktorý má obvod 12 cm. - Trojuholník 49 Trojuholník KLM má dĺžku strán k=6,3cm, l=8,1cm, m=11,1cm. Trojuholník XYZ má dĺžku strán x=8,4cm, y= 10,8cm, z= 14,8cm. Sú trojuholníku KLM a XYZ podobné? (zapíš 0 ak nie, ak áno, nájdi a zapíš koeficient podobnosti)
- Obvod 56
Obvod trojuholníka MAK je 216 mm, strana a=81 mm a strana k=62 mm. Urč dĺžku strany z trojuholníka OSA, ak platí, že trojuholník MAK je zhodný s trojuholníkom OSA.
