Individual 47281
Two resistors, R1 = 300 ohms and R2 = 600 ohms, are connected next. A voltage of 220V is connected. Determine the total resistance by which we can replace both the electric currents passing through the individual resistors and the electric current passing through the unbranched part of the circuit.
Final Answer:

You need to know the following knowledge to solve this word math problem:
themes, topicsGrade of the word problem
Related math problems and questions:
- Two resistors 5
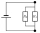 Two resistors are connected in parallel. The first resistor has a resistance of 2000 ohms and a current of 4 mA flows through it. The second resistor has a resistance of 1600 ohms. 1/Draw a circuit diagram 2/Determine the voltage of the power source. 3/Wh
Two resistors are connected in parallel. The first resistor has a resistance of 2000 ohms and a current of 4 mA flows through it. The second resistor has a resistance of 1600 ohms. 1/Draw a circuit diagram 2/Determine the voltage of the power source. 3/Wh - Resistor
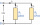 Resistor 1, with a resistance of 100 Ohms, and resistor 2, with a resistance of 400 Ohms, are connected side by side in the circuit. The voltage between the resistor terminals is 80V. a) Draw a circuit diagram and write the entered quantities in it b) Fin
Resistor 1, with a resistance of 100 Ohms, and resistor 2, with a resistance of 400 Ohms, are connected side by side in the circuit. The voltage between the resistor terminals is 80V. a) Draw a circuit diagram and write the entered quantities in it b) Fin - Resistances 66064
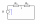 Two resistors with resistances of 40 ohms and 60 ohms are connected in series and connected to a voltage of 150V. A) the total resistance B) current in the circuit C) voltage on both resistors
Two resistors with resistances of 40 ohms and 60 ohms are connected in series and connected to a voltage of 150V. A) the total resistance B) current in the circuit C) voltage on both resistors - Resistance 80351
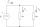 We connected two resistors in parallel in the circuit, with the first having three times the resistance of the second. The voltage between the terminals of each resistor is 6 V. Calculate the current through each branch when the resulting resistance of bo
We connected two resistors in parallel in the circuit, with the first having three times the resistance of the second. The voltage between the terminals of each resistor is 6 V. Calculate the current through each branch when the resulting resistance of bo - Serial resistors
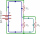 In the circuit shown ( two resistors, R1 and R2, serially connected), the total resistance from A to B is 16 ohms. If the voltage between A and B is 10 V, find the resistance R2 and the current through the R1 = 12-ohm resistor.
In the circuit shown ( two resistors, R1 and R2, serially connected), the total resistance from A to B is 16 ohms. If the voltage between A and B is 10 V, find the resistance R2 and the current through the R1 = 12-ohm resistor. - Resistances 80604
 Resistors with resistances of 6 ohms and 10 ohms are connected in series to a voltage of 24 V. a) How much current passes through them? b) What are the voltages on the individual resistors?
Resistors with resistances of 6 ohms and 10 ohms are connected in series to a voltage of 24 V. a) How much current passes through them? b) What are the voltages on the individual resistors? - Cooker spiral
 A current of 4.4 A flows through the spiral of the electric cooker. It is connected to a voltage of 220 V. What is the resistance of the spiral?
A current of 4.4 A flows through the spiral of the electric cooker. It is connected to a voltage of 220 V. What is the resistance of the spiral?
