Cube-shaped box
Find the size of the smallest possible cube-shaped box where three types of 3cm, 5cm, 6cm small cubes could be stacked to fully use the box space (each type of cube separately). Can you find out how many smallest cubes are in the box?
Correct answer:
Tips for related online calculators
Do you want to calculate the least common multiple of two or more numbers?
Tip: Our volume units converter will help you convert volume units.
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Related math problems and questions:
- Seven segments display
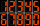Electronic devices sometimes use the type of digits below, where each digit uses some short stripes. For example, seven uses three small stripes. What is the largest three-digit number that you can make if you use twenty stripes? - Twelve flowers
A florist has roses, tulips, daffodils, and carnations to use in flower arrangements. If she were to make an arrangement using 12 flowers, how many different combinations of these four types of flowers would be possible? - A metal
A metal cylinder is inserted into the cube with a 20 cm edge so that the cylinder shell. Its two bases are in close contact with the cube's walls from the inside. How much water could be poured into the free space between the cube and the cylinder so that - Cube-shaped 80585
Boxes with dimensions of 6 cm, 10 cm, and 15 cm should fit into a cube-shaped box. What are the smallest dimensions a box can have? How many boxes of the given dimensions can fit in it? - Measuring 23281
We have a box with dimensions of 20cm, 16cm, and 8cm. How many cubes can fit in it if the cube has a size of 4cm? - Identical 35961
Nine identical spheres are stacked in the cube to fill the volume of the cube as much as possible. What part of the volume will the cube fill? - Minimum surface
Find the length, breadth, and height of the cuboid-shaped box with a minimum surface area, into which 50 cuboid-shaped blocks, each with length, breadth, and height equal to 4 cm, 3 cm, and 2 cm, respectively, can be packed. - Two boxes-cubes
Two boxes of a cube with edges a=28 cm and b = 92 cm are to be replaced by one cube-shaped box (same overall volume). How long will its edge be? - Lamps on playground
The playground has the shape of a rectangle of 36 x 50m. After how many meters can place the lamps on its lighting, if the distances between them are to be the same on both sides if the builders want to use the smallest possible number of lamps? - Three cubes
Two cube-shaped boxes with edges a = 70 cm; b = 90 cm must be replaced by one cube-shaped box. What will be its edge? - Small 7967
How many can small cubes with a 1cm long edge cut from a cube with a 3cm long edge? - Red cubes
There are 15 white and several red cubes in the box. The probability of accidentally pulling out a white cube is 20%. How many red cubes are in the box? - Wedding guests
Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs. - Alcohol 2
Two types of alcohol, one 46% and second 64%, give 16 liters of 54% alcohol. How many liters of each type are in the mixture? - Endless lego set
The endless lego set contains only 6, 9, and 20-kilogram blocks that can no longer be polished or broken. The workers took them to the gym and immediately started building different buildings. And, of course, they wrote down how much the building weighed. - Measuring 26891
What is the smallest square space we can tile with tiles measuring 25 x 15 cm, knowing there will be no need to cut them? How many tiles will we use? - Straightened 26861
A Mazda van with a box body with internal dimensions of 1.6 m x 3.1 m x 1.7 m (w x d x h) with a payload of 1.7 tons delivers crates with pastries. Pastry box 520: dimensions 600mm x 400mm x 200mm (l x w x h), load capacity 15 kg. Calculate: a) How many c
