Trapezoid 15
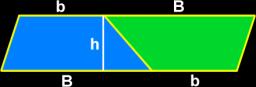
The area of a trapezoid is 266. What value is x if bases b1 is 2x-3, b2 is 2x+1, and height h is x+4
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- expression of a variable from the formula
- arithmetic
- square root
- square (second power, quadratic)
- planimetrics
- area of a shape
- trapezoid
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Trapezium
The lengths of parallel sides of a trapezium are (2x+3) and (x+8), and the distance between them is (x+4). If the area of the trapezium is 590, find the value of x. - Multiple numerical bases
Find the value of x for which 312four+52x=96ten . Hint: four, x, and ten are the base of the given number. - The garden
The garden is an isosceles trapezoid with bases 64 m and 24 m long and a height of 25 m. If a fifth of the area is occupied by a cottage, lawn, and path, in what garden area is it possible to grow vegetables? - Consider 3
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
- Dimensions of the trapezoid
One of the trapezoid bases is one-fifth larger than its height, and the second base is 1 cm larger than its height. Find the dimensions of the trapezoid if its area is 115 cm2 - Parcel
The parcel is rectangular, a trapezoid with bases of 12 m and 10 m and a height of 8 m. On the parcel was a built object with a footprint of an isosceles triangle, with a side of 4 m and a height of three-quarters of a meter. What is the area of the unbui - The size
The size of a Trapezium are 3/4*x cm, x cm, 2*(x+1) cm and 3(x+2) cm long respectively. If its perimeter is 60cm, calculate the length of each side.
