Smoker male
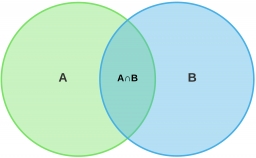
For a person selected randomly from a certain population, events A and B are defined as follows. A = event the person is male B = event the person is a smoker. For this particular population, it is found that P(A ) = 0.53, P(B) = 0.15, and P(A n B ) = 0.18. Find P(A U B ). Round the result to two decimal places.
Correct answer:
Tips for related online calculators
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
combinatoricsalgebrabasic operations and conceptsGrade of the word problem
Related math problems and questions:
- And-or probabilities
P(A ) = 0.53, P(B) = 0.15, and P(A n B ) = 0.18. Find P(A U B ). Round approximations to two decimal places. - Probability 65464
We randomly draw one out of 18 cards with numbers from 1 to 18. What is the probability that the ticket drawn is a prime number? Write the result as a decimal number rounded to two decimal places. - Distribution if the IQ
Assume that the IQ in the population follows a normal distribution with a mean of 100 points and a standard deviation of 10 points. With what probability among 15 randomly selected people: a. Is there anyone with an IQ above 130 points? b. Are there at le - Q10 - investigate A nutritionist who investigates fruits reported that the average weight of a raspberry is 4.4 g with a standard deviation of 1.28 g. What is the probability that a randomly selected raspberry would weigh less than 3.1 grams? Let X represent the weight of
- Population variance
60% of students at a California community college will transfer to a college in the CSU system. The number of students in a sample who will transfer follows a binomial distribution. If eight students are randomly selected, find the population variance σ² - The university
At a certain university, 25% of students are in the business faculty. Of the students in the business faculty, 66% are males. However, only 52% of all students at the university are male. a. What is the probability that a student selected at random in the - Christmas holidays
How many percent take Christmas holidays lasting 18 days from a school year that lasts 303 days? Round the result to two decimal places
