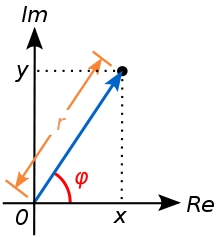
Distance two imaginary numbs
Find the distance between two complex number: z1=(-8+i) and z2=(-1+i).
Correct answer:
Tips for related online calculators
Try our complex numbers calculator.
Do you want to convert length units?
See also our right triangle calculator.
Do you want to convert length units?
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Linear imaginary equation
Given that 2(z+i)=i(z+i) "this is z star" Find the value of the complex number z. - The modulus
Find the modulus of the complex number 2 + 5i - Midpoint between conjugate
Find the midpoint between two roots: 2+3.464i and 2 - 3.464i - Mappings of complex numbers
Find the images of the following points under mappings: z=3-2j w=2zj+j-1 - Complex number coordinates
Which coordinates show the location of -2+3i - An Argand diagram
Find the sum z1+z2 and difference z1-z2 and z2-z1 of z1=5+2i and z2=2+3i by an Argand diagram. - Complex equation
If c - d = 2 and c = 12 + 7 i, find d. Write the result in the form of a + bi. - Find all 2 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
- Alternating circuit
In an alternating circuit, the total voltage V is given by V=V1 +V2 If V=(12.2+6.8i) V and V1=(7.8-2.5i) V, find the voltage V2. - Complex plane mapping
Show that the mapping w = z +c/z, where z = x+iy, w = u+iv, and c is a real number, maps the circle |z| = 1 in the z-plane into an ellipse in the (u, v) plane. - Quadratic 21643
Solve the quadratic equation: 2y²-8y + 12 = 0 - Suppose 5
Suppose z5=2+3i and z6=6+9i are complex numbers and 3 z5 + 7 z6= m+in. What is the value of m and n? - Imaginary numbers
Find two imaginary numbers whose sum is a real number. How are the two imaginary numbers related? What is their sum? - Real and imaginary parts
Let z1=x1+y1i and z2=x2+y2i Find: a = Im (z1z2) b = Re (z1/z2) - Trapezium
The lengths of parallel sides of a trapezium are (2x+3) and (x+8), and the distance between them is (x+4). If the area of the trapezium is 590, find the value of x. - Goniometric form
Determine the goniometric form of a complex number z = √ 110 +4 i. - Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
