ABCD
AC= 40cm , angle DAB=38 , angle DCB=58 , angle DBC=90 , DB is perpendicular on AC , find BD and AD
Final Answer:

Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The quadrilateral
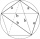 The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right.
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - Diagonal BD
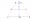 Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42°
Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42° - Angles
 In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β?
In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β? - ABCD rhombus
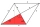 ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree.
ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree. - Parallelogram - angle alfa
 In the parallelogram ABCD the length of sides are AB = 8, BC = 5, BD = 7. Calculate the magnitude of the angle α = ∠DAB (in degrees).
In the parallelogram ABCD the length of sides are AB = 8, BC = 5, BD = 7. Calculate the magnitude of the angle α = ∠DAB (in degrees). - MO - triangles
 On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
