Trapezoids
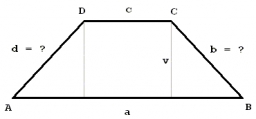
In the isosceles trapezoid ABCD we know: AB||CD, |CD| = c = 8 cm, height h = 7 cm, |∠CAB| = 35°. Find the area of the trapezoid.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Base RR odd
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - Trapezoid 70454
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Isosceles 37621
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Rectangle ABCD
The rectangle ABCD is given whose | AB | = 5 cm, | AC | = 8 cm, ∢ | CAB | = 30°. How long is the other side, and what is its area?
- Trapezoid 20873
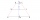In the trapezoid ABCD (AB II CD) is α = 57 °, γ = 4β. Calculate the size of all interior angles. - Isosceles Isosceles trapezoid ABCD has a perimeter of 39 cm. The base AB is 7 cm longer than the base CD and the arm is 2 cm shorter than the base CD. Calculate the length of the base CD.
- Isosceles trapezoid
Isosceles trapezoid ABCD, AB||CD is given by |CD| = c = 12 cm, height v = 5 cm and |CAB| = 41°. Calculate area of the trapezoid.
